【Python】A/Bテストの結果をピアソンのカイ二乗検定（独立性の検定）で紐解く

こんにちは、データサイエンティストのたぬ（@tanuhack）です！

Web業界で働いていれば、耳にタコができるくらい聞き飽きた『A/Bテスト（ランダム化比較試験）』という言葉。果たして、一体どれくらいの組織が正しくA/Bテストの結果を分析し、次のアクションに繋げられているのでしょうか…。

例えば、次のクロス集計表を見て、「うぉっしゃ、広告Bイケるやん！！！追加で広告費つぎこんだろー！！！」と、真っ先に思い浮かんだ方は要注意です。

chi2test_demo1 — CV（購入した）、Not CV（購入していない）

このクロス集計表で言えば、Aの購入率は『11.64％』で、Bの購入率は『13.47%』なので、一見するとBの方が優れて見えますよね。

でも、ここには『誤差』という見えない落とし穴が存在します。

そこで今回は、こうしたクロス集計表について、『意味のある偏り』なのか、『誤差でもこれくらいの差は生じるのか』といったことを確かめるために、統計学の『カイ二乗検定』をPythonで実装し確認する方法を紹介します！

1 Pythonでカイ二乗検定を使う準備
2 Pythonでカイ二乗検定を行う
- 2.1 scipy.statsのchi2_contingency関数を使う
- 2.2 動作を確認する
3 さいごに

Pythonでカイ二乗検定を使う準備

必要なライブラリをインポート

クロス集計表を作成するためにPandasと、カイ二乗検定を行うためにSciPyをインポートします。

import pandas as pd
import scipy as sp

クロス集計表を作成する

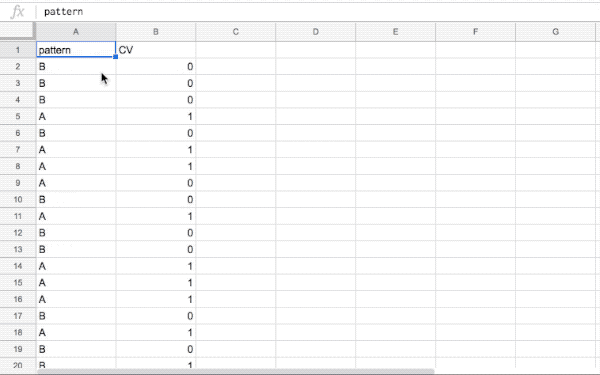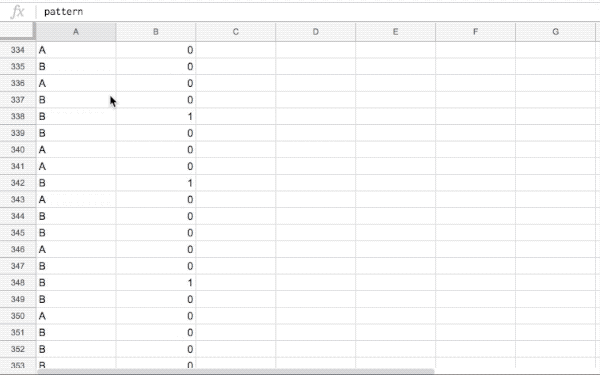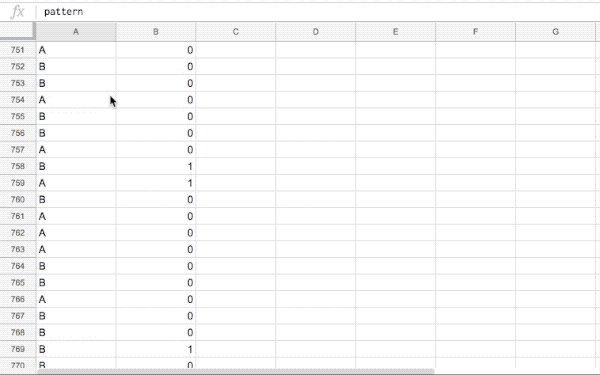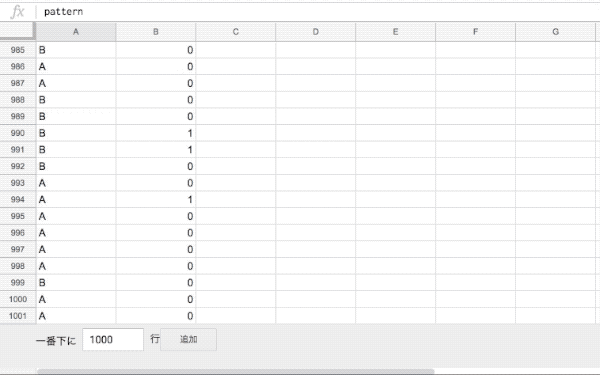
実務では、CSVファイルやスプレッドシートをPandasのDataFrameとして取り込んで、クロス集計表を作る流れが多いと思うので、それに沿って紹介します。

今回は、『chi2test_demo.csv』というCSVファイルを取り込んだものとして話を進めますね。

df = pd.read_csv('chi2test_demo.csv')

【Python】PandasでCSVファイルを読み込み/書き出しする実践テクニック集

[データI/O]スプレッドシート×DataFrameを一気に変換する方法

chi2test_demo.csvサンプル（※飛び先はCSVではなく、スプレッドシートです。）

A列	B列
パターン（AまたはB）	CV（申し込み）があったら1、なければ0

pd.crosstab()でクロス集計表を作成する

Pandasのcrosstab関数でクロス集計表を作ることが出来ます。

df_cross = pd.crosstab(index=df['pattern'], columns=df['CV'])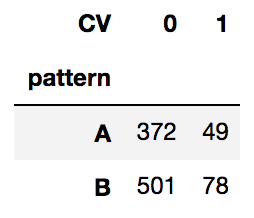

【おまけ】CSVを読み込まず、クロス集計表を直接作成する

場合によっては、あらかじめクロス集計されているものもあるかと思います。

その場合は、普通にPandasのDataFrame関数でクロス集計表を作りましょう。

df_cross = pd.DataFrame(
    [[372,49],[501,78]],
    index=['A', 'B'],
    columns=['CV', 'Not CV']
)

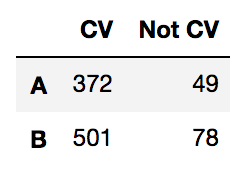
仮説を立てる

このクロス集計表で言えば、Aの購入率は『11.64％』で、Bの購入率は『13.47%』なので、一見するとBの方が優れて見える。

広告AとBに統計的な有意な差があるのか、カイ二乗検定を使って検証してみよう。

仮説

帰無仮説 $H_0$ ：広告(A,B)とCV(購入数)は独立である（関連がない）
対立仮説 $H_1$ ：広告(A,B)とCV(購入数)は独立ではない（関連がある）

また、p値の有意水準は慣例的に『0.05』とします。

Pythonでカイ二乗検定を行う

カイ二乗検定では、『期待度数と観測度数の乖離』を計算することで独立性の検定を行います。

具体的には、次式に表している $\chi^2$ 統計量を基に、自由度kのカイ二乗分布に従って判断します。

$\chi^2 = \sum_{i}\sum_{j}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}$

ここで、 $O_{ij}$ と $E_{ij}$ は、それぞれ観測度数と期待度数のi行j列目の成分を表しています。

Pythonでカイ二乗検定をする場合、この面倒な計算を全部すっ飛ばして、 $\chi^2$ 統計量やp値、自由度など、まとめて算出することが出来るので、その方法を見てみましょう。

scipy.statsのchi2_contingency関数を使う

Pythonでカイ二乗検定を行う場合、scipy.statsのchi2_contingency関数を使います。scipy.stats.chi2_contingency｜公式サイト(英語)

chi2, p, dof, ef =  scipy.stats.chi2_contingency(df, correction=False)

結果は、 $\chi^2$ 統計量、p値、自由度、期待度数の表の順に出力されます。

標準だと、※イェイツの修正が入るので、correction=Falseとして、余計な補正が入らないように設定しましょう。

イェイツの修正(本文の一部を抜粋)

主に分割表の中の少なくとも一つの期待度数が5より小さい場合に用いられる。不幸なことに、イェイツの修正は修正しすぎる傾向があり、このことは全体として控えめな結果となり帰無仮説を棄却すべき時に棄却し損なってしまうことになりえる(第2種の過誤)。そのため、イェイツの修正はデータ数が非常に少ない時でさえも必要ないのではないかとも提案されている

出典：『イェイツのカイ二乗検定｜Wikipedia』

動作を確認する

import pandas as pd
import scipy as sp

df = pd.read_csv('chi2test_demo.csv')
df_cross = pd.crosstab(index=df['pattern'], columns=df['CV'])

chi2, p, dof, ef =  sp.stats.chi2_contingency(df_cross, correction=False)
chi2, p, dof, ef

出力

(0.7383347016905837, 0.39019485527762676, 1, array([[367.533, 53.467],[505.467, 73.533]]))

2つ目の配列の値が今回知りたいp値(0.39019485527762676)です。

p値の値が0.05を大きく超えているので、帰無仮説 $H_0$ は採択されることになり、残念ながら広告Aと広告Bに有意な差は認められない結論になりました。

この分析結果から、広告Bにアクセルを踏んで巨額の広告費を掛けない方が無難であるという経営上の判断が出来ます。（CVRが2%近く離れているのに、有意差が無いなんて残酷ですね。）

さいごに

今回は、Pythonを使ってA/Bテストの結果を正しく見る方法を紹介しました。

『誤差を理解し、誤差を踏まえたうえでも意味あるA/Bテストだったか』という統計学の考えを身につければ、なあなあでA/Bテストをやってた部分だったり、怪しい統計データをウソと見抜けたり、良いことだらけです。

それでは