Pythonのttest_1sampで1標本t検定(両側/片側検定)を行う方法

こんにちは、データサイエンティストのたぬ（@tanuhack）です！

母分散が未知で、より現実的な正規分布の母平均の検定は、1標本のt検定と呼ばています。

これは『t検定統計量』と呼ばれるを検定統計量として使い、自由度n-1の『t分布』に従わせ、ビジネス上では主にA/Bテストの検証に用いられることが多いです。

数式が複雑で面倒な計算も、Pythonならちょちょいのちょい。

ということで今回は、Pythonを使って1標本t検定(両側/片側検定)を行う方法を紹介します！

この記事の著者

データサイエンティスト / ブロガー

たぬ

tanu

詳しいプロフィール

プロフィール

福岡在住のデータサイエンティスト。Pythonでルーチンワークを瞬殺する仕組みを作ることやデータを視覚化することが得意です。

Pythonで実装する1標本t検定の流れ

仮説の設定

Pythonで1標本t検定(両側/片側検定)を行う

Pythonで1標本t検定を行うためには、SciPyのscipy.stats.ttest_1sampメソッドを使います。1sampは1標本の略だと思われ。scipy.stats.ttest_1samp｜公式サイト（英語）

scipy.stats.ttest_1sampメソッドを使えば、両側検定だろうが片側検定だろうが、一発で分かるので重宝しています。

t, p = sp.stats.ttest_1samp(a, popmean)

ttest_1sampメソッドを使うと、2つの値(t値, p値)が格納されたタプルが返されるので、t検定で判断すべき数字は後者になります。

import numpy as np
import scipy as sp

coffee = np.array([
    210.9, 195.4, 202.1 , 211.3, 195.5, 
    212.9, 210.9, 198.3, 202.1, 215.6, 
    204.7, 212.2, 200.7, 206.1, 195.8
])

t, p = sp.stats.ttest_1samp(coffee, popmean=200)
print('母平均が200のt値：'+str(t))
print('母平均が200である確率(p値)：'+str(p))

今回の場合、p値の値が1.5％だったので、両側検定でも片側検定でも共に帰無仮説が棄却され、対立仮説が成り立ちます。

(余談ですが、片側検定の方が帰無仮説を棄却させやすいです)

1標本t分布をグラフで直感的に理解する

SciPyのscipy.stats.ttest_1sampメソッドで簡単に1標本t検定で使用するp値が得られました。

でも、このままだと、直感的にイメージが付きにくいと思いませんか？？

ということで、先程得られたt値とp値を使って、matplotlibを使ってt分布を描画し、視覚的に帰無仮説を棄却できているのか確認してみましょう。

両側検定の場合

import numpy as np
import scipy as sp
from matplotlib import pyplot as plt

coffee = np.array([
    210.9, 195.4, 202.1 , 211.3, 195.5, 
    212.9, 210.9, 198.3, 202.1, 215.6, 
    204.7, 212.2, 200.7, 206.1, 195.8
])

# 検定統計量
n = len(coffee)                 # サンプル数
k = n-1                         # 自由度
u_var = np.var(coffee, ddof=1)  # 不偏分散
s_mean = np.mean(coffee)        # 標本平均

# t値とp値を求める
t, p = sp.stats.ttest_1samp(coffee, popmean=200)

# ここからグラフ描画
############################
x = np.linspace(-6, 6, 1000)
fig,ax = plt.subplots(1,1)

# t分布を描画する
ax.plot(x, sp.stats.t.pdf(x, k), linestyle='-', label='k='+str(k))

#　t分布に今回の確率分布を表示させる
ax.plot(t, p, 'x', color='red', markersize=7, markeredgewidth=2, alpha=0.8, label='experiment')

# t分布の95%信頼区間から外れた領域を描画する
bottom, up = sp.stats.norm.interval(alpha=0.95, loc=0, scale=1)
plt.fill_between(x, sp.stats.t.pdf(x, k), 0, where=(x>=up)|(x<=bottom), facecolor='black', alpha=0.1)

plt.xlim(-6, 6)
plt.ylim(0, 0.4)
 
plt.legend()
plt.show()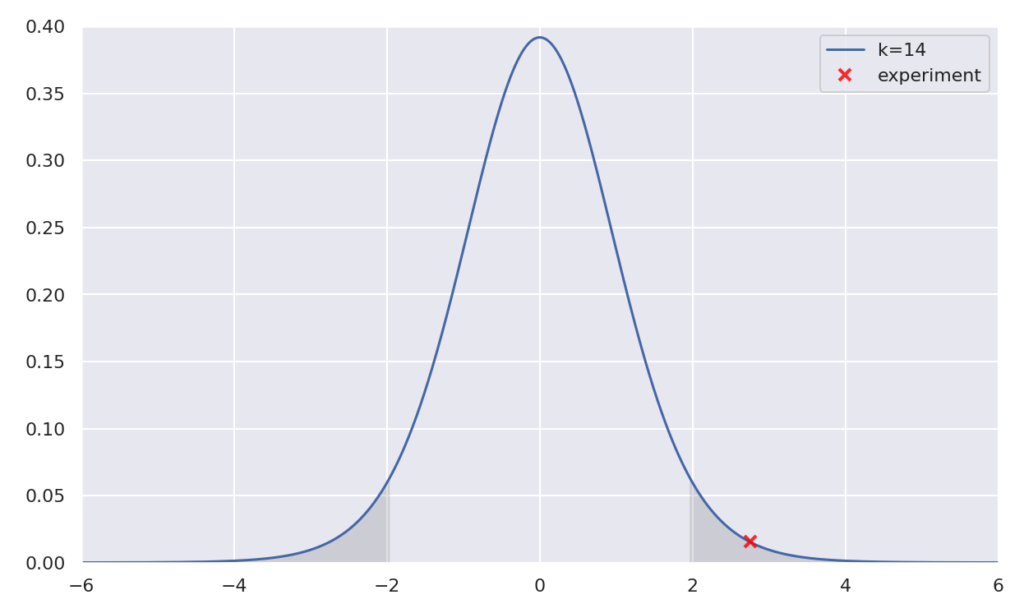

グラフを見ての通り、ちゃんと95％信頼区間以外に存在しているので、帰無仮説が棄却され、対立仮説が成り立ちます。

片側検定（上側）の場合

import numpy as np
import scipy as sp
from matplotlib import pyplot as plt

coffee = np.array([
    210.9, 195.4, 202.1 , 211.3, 195.5, 
    212.9, 210.9, 198.3, 202.1, 215.6, 
    204.7, 212.2, 200.7, 206.1, 195.8
])

# 検定統計量
n = len(coffee)                 # サンプル数
k = n-1                         # 自由度
u_var = np.var(coffee, ddof=1)  # 不偏分散
s_mean = np.mean(coffee)        # 標本平均

# t値とp値を求める
t, p = sp.stats.ttest_1samp(coffee, popmean=200)

# ここからグラフ描画
############################
x = np.linspace(-6, 6, 1000)
fig,ax = plt.subplots(1,1)

# t分布を描画する
ax.plot(x, sp.stats.t.pdf(x, k), linestyle='-', label='k='+str(k))

#　t分布に今回の確率分布を表示させる
ax.plot(t, p, 'x', color='red', markersize=7, markeredgewidth=2, alpha=0.8, label='experiment')

# t分布の90%信頼区間から外れた領域を描画する
bottom, up = sp.stats.norm.interval(alpha=0.90, loc=0, scale=1)
plt.fill_between(x, sp.stats.t.pdf(x, k), 0, where=(x>=up), facecolor='black', alpha=0.1)

plt.xlim(-6, 6)
plt.ylim(0, 0.4)
 
plt.legend()
plt.show()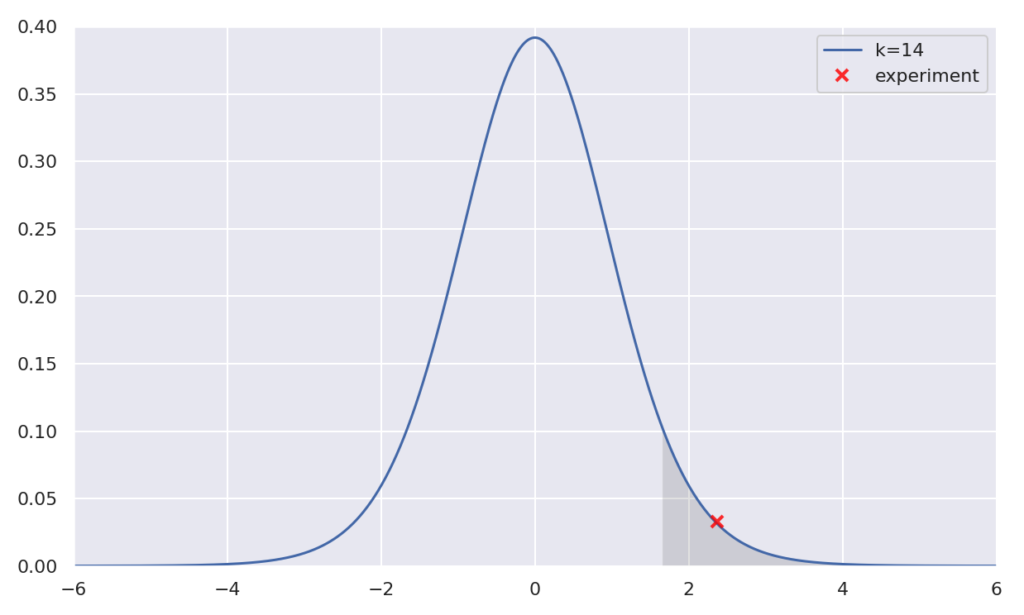

こちらもグラフを見ての通り、ちゃんと95％信頼区間以外に存在しているので、帰無仮説が棄却され、対立仮説が成り立ちます。

片側検定の下側を確認したい場合はプログラムを以下のように修正して下さい。

plt.fill_between(x, sp.stats.t.pdf(x, k), 0, where=(x<=bottom), facecolor='black', alpha=0.1)