こんにちは、データサイエンティストのたぬ(@tanuhack)です!
ビジネスで分析をしていると、商品Aが売れた売れなかった、商品Bが売れた売れなかったなどをパッと確認できるように、次のようなクロス集計表を作成することが多々あると思います。
| 購入された | 購入されなかった | 購入率(%) | |
|---|---|---|---|
| 商品A | 72 | 3,217 | 2.18 |
| 商品B | 69 | 3,499 | 1.93 |
この数字を見せられると誰もが、商品Aの方が商品Bより購入率が0.25%優れていると判断し、今後は商品Aを売るための施策を考える機会が増えるでしょう。
果たして、その判断で大丈夫なのでしょうか…。
結論から言うと×です。何故かと言うと、クロス集計表だけでは、見えない『誤差』までは補えないからです。
そこで今回は、こういったクロス集計表の誤差まで考慮して、経営判断の助けになる統計学の『カイ二乗検定』をスプレッドシートで行う方法を紹介します。
目次
ピアソンのカイ二乗検定
カイ二乗検定では、『期待度数と観測度数の乖離』を計算することで独立性の検定を行います。
2つ以上の分類基準を持つクロス集計表において、分類基準間に関連があるかどうかを検定することです。
今回の例で言うと、商品A、Bと購入率に影響があるのか確認します。
通常の統計学であれば、次式に表している統計量を基に、自由度kのカイ二乗分布に従って判断します。(ここで、
と
は、それぞれ観測度数と期待度数のi行j列目の成分を表しています。)
ただ、スプレッドシートでカイ二乗検定をする場合、この面倒な計算を全部すっ飛ばして、『期待度数表』と『観測度数表』を作るだけで、カイ二乗検定をすることができます!!
なので、期待度数表と観測度数表をさっそく作ってみましょう。
スプレッドシートでカイ二乗検定
観測度数表を作る
観測度数表とは、実際の観測度を表に当てはめ、クロス集計表を作成することです。
STEP1:スプレッドシートに観測度を入力する
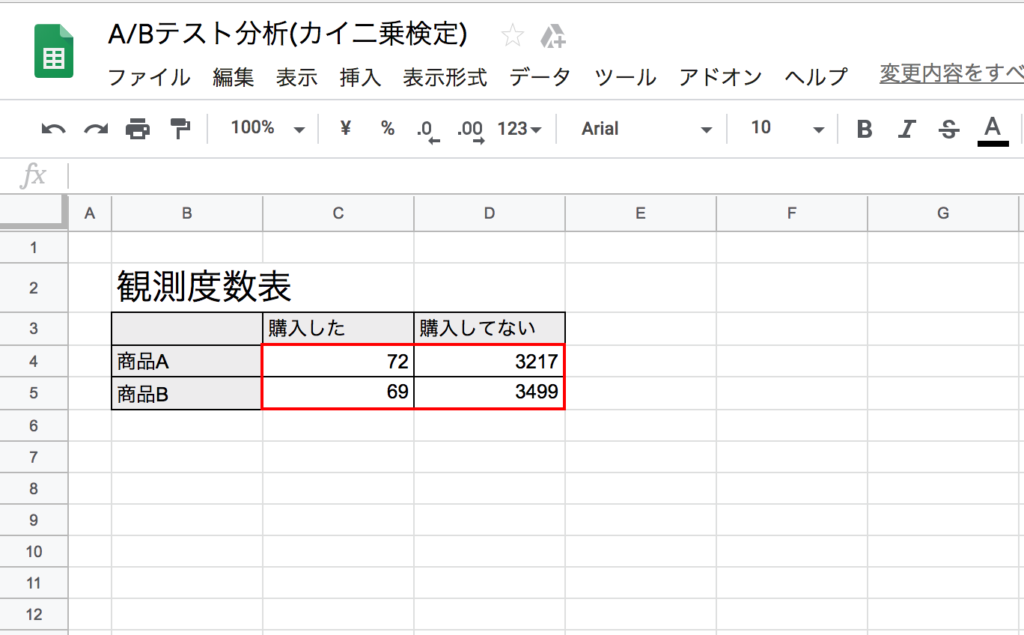
ここでは、分かりやすく赤枠に実際の観測度を入力しています。
STEP2:各項目の合計の列を作る
スプレッドシートで作成すると次の画像のようになります。
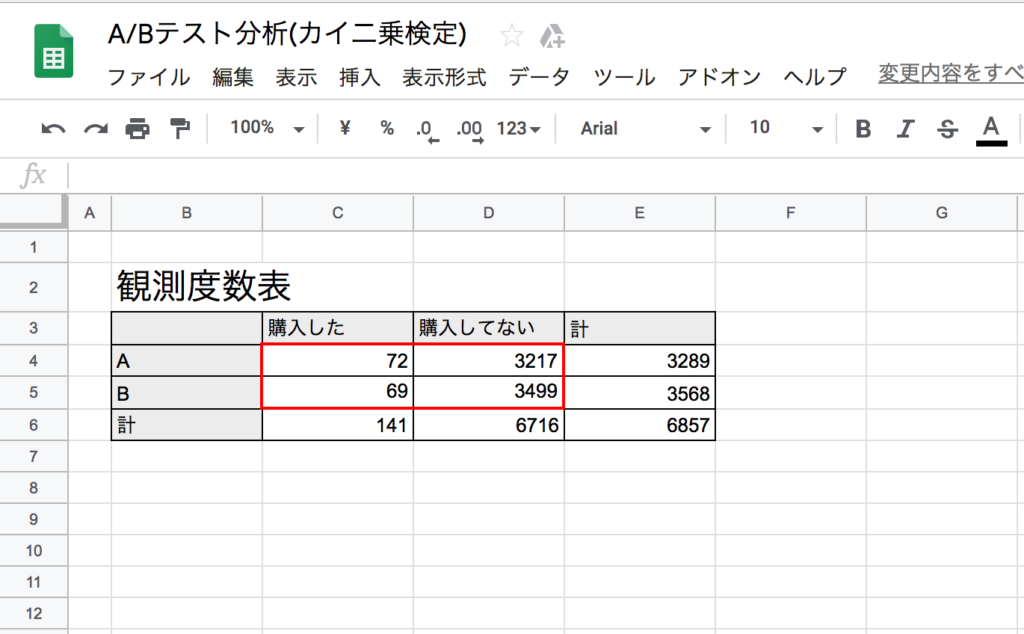
これで、観測度数表は完成です!
期待度数表を作る
先程も紹介したように、カイ二乗検定(独立性の検定)では『実測値(観測値)』を『理論値(期待値)』と比較します。
今出ているのは、観測度数表なので、『理論値(期待値)』を算出する必要があります。例えば、今回だと、商品AとBの間の購入率の理想比率は1:1です。
各セルの理論値(期待値)は観測度数表を使って算出します。

商品A かつ 購入した
商品A かつ 購入してない
商品B かつ 購入した
商品B かつ 購入してない
上記の数式をそれぞれのセルに代入してもいいですが、サクッとARRAYFORMULA関数で計算させましょう。
=ARRAYFORMULA(縦の合計列×横の合計行/総サンプル数)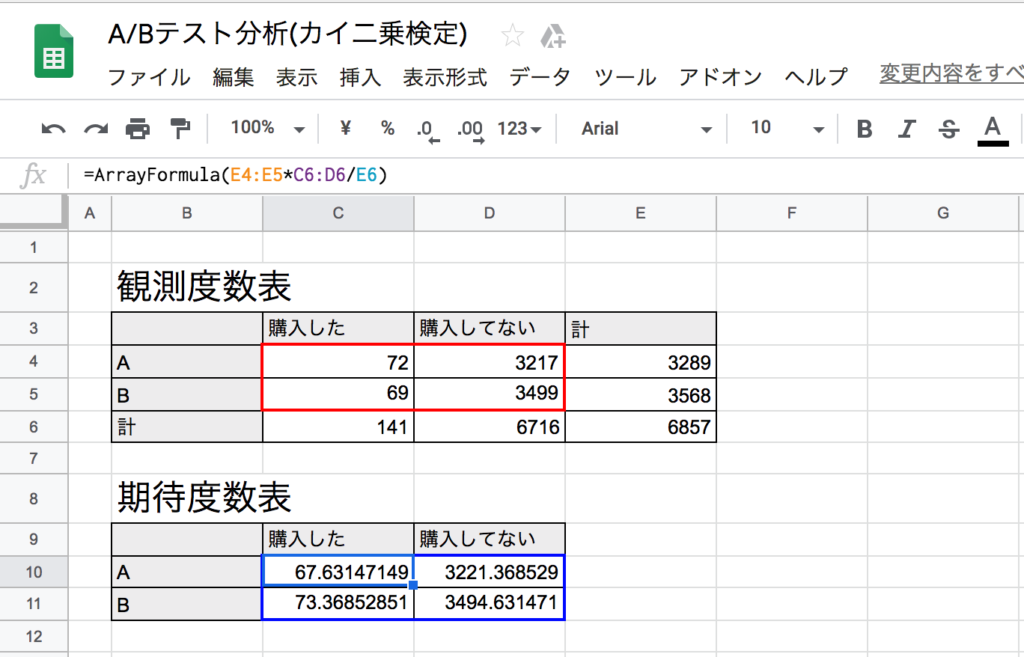
=ARRAYFORMULA(E4:E5*C6:D6/E6) スプレッドシートの『ARRAYFORMULA』関数を使って表示速度を高速化させよう!
スプレッドシートの『ARRAYFORMULA』関数を使って表示速度を高速化させよう!
これで、期待度数表も完成です!
chitest関数でピアソンのカイ二乗検定
スプレッドシートでピアソンのカイ二乗検定を行う場合、CHITEST関数を使います。
=CHITEST(観測度数表, 期待度数表)この数式を実行すると2つのデータ範囲をもとにピアソンのカイ二乗検定を行い、その確率を返します。
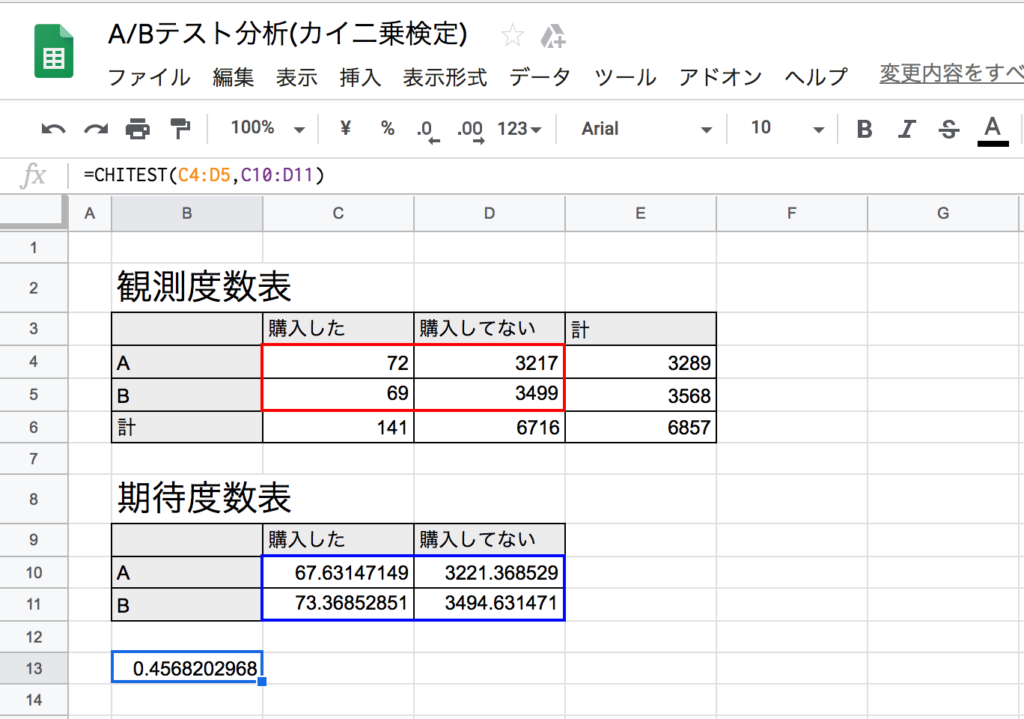
=CHITEST(C4:D5,C10:D11)結果、求められた確率0.4568202968は、有意水準の0.05%よりも遥かに大きかったので、商品Aの方が商品Bより優れているとは言えませんでした。(※誤差が45%も含まれています。)
カイ二乗検定の注意点
2行×2列のカイ二乗検定において、期待度数表の4マスのうち1マス(25%)でも期待数『5未満』があればその時点で「20%以上が5未満」を満たしてしまうためカイ2乗検定を用いることは不適切となります。(コクラン・ルール)
特に2行×2列のカイ二乗検定では、すべての期待度数表の値が10以上である方が精度が保証され、正しい確率を求める事ができます。
もし、期待度数表に5以下の値が出た場合は『フィッシャーの正確検定』を用いれば求めることができます。
フィッシャーの正確検定
2行×2列のクロス集計表における行要素と列要素の関連の強さを示す指標。行の合計と列の合計を一定とみなし、起こりうる全てのケースのうち観測度数より稀なケースが発生する確率を直接計算して求める。
2行×2列のクロス集計表の各セルの値を以下のようにa, b, c, d, nを用いて表したとき、この組み合わせが得られる確率pは超幾何分布を用いて下式から求めることができる。
1つ注意なければいけないのが、スプレッドシート上でフィッシャーの正確検定を行う場合、計算できる数字の有効桁数が少ないので、オーバーフローが発生します。(階乗の計算がヤバいので…。)
さいごに
今回は、スプレッドシートを使ってカイ二乗検定を行う方法を紹介しました。
本来データ分析はPythonでやるべきですが、ミクロなものに関してはキリがないと思うので、そういうものに対してはスプレッドシートで統計をやってもいいと思います。共有簡単ですしね。
 【Python】A/Bテストの結果をピアソンのカイ二乗検定(独立性の検定)で紐解く
【Python】A/Bテストの結果をピアソンのカイ二乗検定(独立性の検定)で紐解く
クロス集計表を作って、ハイ、おしまい。ではなく、きちんと統計的に誤差がないのかまで考えて確実なものにしましょう。
それでは



